Inverse or Optimization Problems for Multiple (Ellipse) Ellipsoid Configurations

This academic test case was developed in order to study algorithmic convergence by splitting the inverse problem (recovery of target pressure on the surface) into smaller subproblems. It also provides a way to study the behaviour of algorithms with meshes of different quality. Finally, it can be expanded into a simple test platform for multiphysics optimization (computational fluid dynamics, computational electromagnetism, and aeroacoustics), both in 2D and 3D.

Objectives:
Aerodynamic reconstruction problem
Recovery of the original position of two ellipses (2D) or ellipsoids (3D) using potential, Euler, or turbulent Navier-Stokes flows.

CEM radar wave problem
RCS optimization using perfectly conducting or coated material (under development).

CAA wave problem
Noise prediction and reduction (under development).

Requirements: Navier-Stokes solver, acoustics solver, Maxwell solver
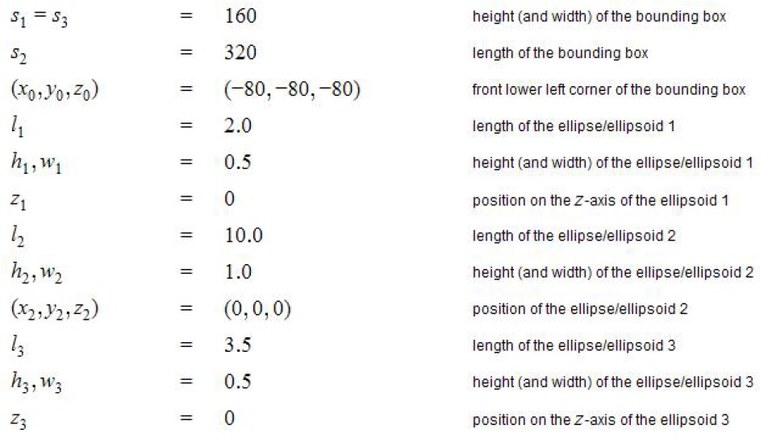
Computational domain: See the figure for the 2D case.

Modeling: physical properties:
Aerodynamic reconstruction problem
- Incompressible fluid (Navier-Stokes turbulent flow).
- Kinematic viscosity V = 1/100.

Boundary and/or initial conditions for computations:
Aerodynamic reconstruction problem
Upstream entrance: u = 1.0, angle of attack a = 3.0º
Downstream exit: free boundary conditions
Ellipse/ellipsoid surface: no-slip condition

Material Parameters:
Solid
Fluid

Optimization:
Aerodynamic reconstruction problem

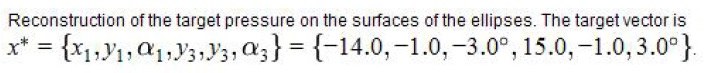
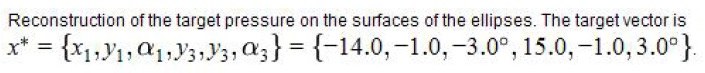
Results:
Aerodynamic reconstruction problem
- Pressure contours of the best solution
- Final mesh
- Averaged convergence curves of the tested algorithms
- For the tested algorithms the following values are required

• mean final value
• standard deviation
• minimum value
• maximum value
• average number of fitness calculations required

-

Defined by Jyri Leskinen, 2006.